
Example: Kirchhoff's Rules
The rules become clearer if you see how to
apply them to one or two concrete situations.
Let us start with a simple example first :
Question:
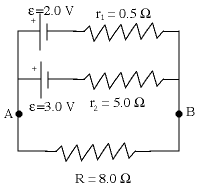 In
order to increase the capacity to deliver current, one often puts
two batteries in parallel. Consider a
battery with e1 = 2.0 V,
internal resistance r1 = 0.5 W,
put in parallel with another battery with e2
= 3.0 V, internal resistance r2 = 5 W
. A and B
are the terminals of the
composite battery so produced. Suppose an external resistance of R
= 8 W is connected across AB. What is
the effective terminal voltage of the battery, VAB, and
the current through R?
In
order to increase the capacity to deliver current, one often puts
two batteries in parallel. Consider a
battery with e1 = 2.0 V,
internal resistance r1 = 0.5 W,
put in parallel with another battery with e2
= 3.0 V, internal resistance r2 = 5 W
. A and B
are the terminals of the
composite battery so produced. Suppose an external resistance of R
= 8 W is connected across AB. What is
the effective terminal voltage of the battery, VAB, and
the current through R?
Answer:
- Assume the currents through the three horizontal lines to be
I1, I2 and I. At this moment, we assume each
of them to be right to left as shown. In case any of them has the
opposite sense, it will turn out to be negative when we finally
calculate it from the equations.
- When a current goes through a resistor, it must flow from high
to low voltage. So the right side of each resistor is higher than
the left (for the current direction arbitrarily chosen) as is
shown by the red + and
-.
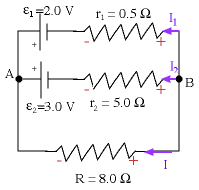
- Apply Rule 1 to the junction A. Usually the sign
convention for currents is that it is positive if
going into a junction, and negative if going out. [You
could make the opposite convention too, just as long as you are
consistent.]
at junction A, => I1 + I2 + I =
0
- Now apply Rule 2 to the loop e1ARBe1
going around counterclockwise starting at A:
I ·( 8 W ) -
I1·( 0.5 W ) + 2.0 V =
0
Again, applying Rule 2 to the loop e2ARBe2
:
( I )·( 8 W ) -
I2·( 5.0 W ) + 3.0
V=0
- Rearranging these three equations,
I1 + I2 + I =
0
8·I - 0.5·I1 = -2 A
8·I - 5.0·I2 = -3 A
This is set of three equations for three unknowns! The rest of
the steps deal with the solution of this system. Among the many
possibilities, here is one solution:
- Replace I in the second two equations by -(I1 +
I2).
-8.0·(I1 + I2) -
0.5·I1 = -8.5·I1 -
8.0·I2 = -2 A
-8.0·(I1 + I2) -
5.0·I2 = -8.0·I1 -
13.0·I2= -3 A
- Solve: You can multiply the bottom equation by 8 and the top
equation by 13:
13(-8.5·I1 - 8.0·I2) =
13(-2 A) => -110.5 I1 - 104·I2 = -26
A
8(-8.0·I1 -
13.0·I2) = 8(-3 A) => -64 I1 -
104·I2 = -24 A)
Now subtract the first from the second equation. Result:
(110.5 - 64) I1 = 2 A => I1 =
0.043 A
Now plug this into the first equation (or second equation) and
get
I2 = 0.2043 A.
This gives
I = -I1 - I2 = -0.2473
A
- The minus sign in this result shows that the current I flows
opposite to the direction chosen in the diagram.
- The absolute value of the voltage drop between points A and B
(across our composite battery) is
- I R = (0.2473 A)·(8.0 W)
= 1.9784 V,
where we have to keep in mind that point A is at a higher
potential than point B.
©
MultiMedia
Physics
2000


In order to increase the capacity to deliver current, one often puts two batteries in parallel. Consider a battery with e1 = 2.0 V, internal resistance r1 = 0.5 W, put in parallel with another battery with e2 = 3.0 V, internal resistance r2 = 5 W . A and B are the terminals of the composite battery so produced. Suppose an external resistance of R = 8 W is connected across AB. What is the effective terminal voltage of the battery, VAB, and the current through R?
