Battery
 To
run many of our household appliances we take the energy from a wall
socket. We may also supply the energy from a battery, which
continuously converts chemical energy into electrical energy and
supplies it to the circuit to compensate for the energy lost to
dissipation.
To
run many of our household appliances we take the energy from a wall
socket. We may also supply the energy from a battery, which
continuously converts chemical energy into electrical energy and
supplies it to the circuit to compensate for the energy lost to
dissipation.
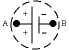 A
battery is a device that holds a fixed potential difference V between
its two terminals, A and B. The conventional assignment of + at
terminal A and - at terminal B is indicated in the picture on the
right. Chemical reactions in the electrolyte inside the battery drive
positive ions to move towards the electrode A, and negative charges
towards the electrode B. This results in an accumulation of positive
charges on A, and negative charges on B. The accumulation process
stops when the force on a charge due to the potential difference in
the electrolyte resulting from this accumulation exactly equals the
force due to the chemical reaction driving it to the electrodes.
A
battery is a device that holds a fixed potential difference V between
its two terminals, A and B. The conventional assignment of + at
terminal A and - at terminal B is indicated in the picture on the
right. Chemical reactions in the electrolyte inside the battery drive
positive ions to move towards the electrode A, and negative charges
towards the electrode B. This results in an accumulation of positive
charges on A, and negative charges on B. The accumulation process
stops when the force on a charge due to the potential difference in
the electrolyte resulting from this accumulation exactly equals the
force due to the chemical reaction driving it to the electrodes.
When a wire is connected between A and B, this potential
difference creates a field in the wire, moving electrons from B to A
through the wire. For each electron that moves from B to A through
the wire and neutralizes one unit of positive charge on A, the
chemical reaction supplies a positive ion to A, and the process keeps
going on and on.
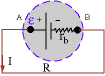 The
open-circuit voltage, i.e. the potential difference between A and B
when no current is drawn by connecting the wire, is called the
electromotive force, or
emf.
We denote it by e. When a
current flows through the battery, the
terminal
voltage = VA - VB is usually
less than e. This is because of the
internal resistance,
rb, of the battery. From the diagram, it is clear that the
resistance of the wire (and whatever devices connected to the wire),
R, and rb are in series (the same
current I flows through them). Then
The
open-circuit voltage, i.e. the potential difference between A and B
when no current is drawn by connecting the wire, is called the
electromotive force, or
emf.
We denote it by e. When a
current flows through the battery, the
terminal
voltage = VA - VB is usually
less than e. This is because of the
internal resistance,
rb, of the battery. From the diagram, it is clear that the
resistance of the wire (and whatever devices connected to the wire),
R, and rb are in series (the same
current I flows through them). Then
$\epsilon$ = I $\cdot$ ( R + rb
)
which means that the terminal voltage
V = I $\cdot$ R = $\epsilon$-
I$\cdot$ rb
Example:
Typical flashlight batteries have emf. = 1.50 V, but a
relatively high internal resistance, say rb = 3
$\Omega$. So when a current of 50 mA is drawn
from it, its terminal voltage will be 1.50 V -
(50$\cdot$ 10-3 A)$\cdot$ ( 3 $\Omega$
) = 1.50 - .15 V = 1.35 V. However, a car battery, made from lead
and acid, has a rather low internal resistance, say rb
= 0.01 $\Omega$. Its emf of a single lead/acid
cell is usually 2.00 V, so even when a relatively high current of
5 A is drawn, it gives a terminal voltage of 2.00 - (5$\cdot$ 0.01)
V = 1.95 V.
However, for most purposes in this class, the distinction between
the terminal voltage, V, and the electromotive force, $\epsilon$,
is not important, and we will usually use V instead of $\epsilon$.
Points to remember:
- A battery has two important characteristics : emf.,
$\epsilon$, and internal resistance
rb.
- The emf. is determined by its chemical constituents : the
material of the two electrodes, and the material of the
electrolyte.
- The internal resistance is determined by features of its
construction, like the distance between the plates, and the common
area of the plates facing each other.
- The maximum terminal
voltage one can get from a battery is its emf., $\epsilon$.
- The maximum current that a battery can deliver is its
short circuit current
(i.e., current when the external resistance is made 0), which is
$\epsilon$/ rb .
- Caution: the symbol
that one uses for the electromotive force, $\epsilon$,
is the same as that for the permittivity.
Please make sure that you do not confuse these two
quantities.
©
MultiMedia
Physics
2000
 To
run many of our household appliances we take the energy from a wall
socket. We may also supply the energy from a battery, which
continuously converts chemical energy into electrical energy and
supplies it to the circuit to compensate for the energy lost to
dissipation.
To
run many of our household appliances we take the energy from a wall
socket. We may also supply the energy from a battery, which
continuously converts chemical energy into electrical energy and
supplies it to the circuit to compensate for the energy lost to
dissipation. A
battery is a device that holds a fixed potential difference V between
its two terminals, A and B. The conventional assignment of + at
terminal A and - at terminal B is indicated in the picture on the
right. Chemical reactions in the electrolyte inside the battery drive
positive ions to move towards the electrode A, and negative charges
towards the electrode B. This results in an accumulation of positive
charges on A, and negative charges on B. The accumulation process
stops when the force on a charge due to the potential difference in
the electrolyte resulting from this accumulation exactly equals the
force due to the chemical reaction driving it to the electrodes.
A
battery is a device that holds a fixed potential difference V between
its two terminals, A and B. The conventional assignment of + at
terminal A and - at terminal B is indicated in the picture on the
right. Chemical reactions in the electrolyte inside the battery drive
positive ions to move towards the electrode A, and negative charges
towards the electrode B. This results in an accumulation of positive
charges on A, and negative charges on B. The accumulation process
stops when the force on a charge due to the potential difference in
the electrolyte resulting from this accumulation exactly equals the
force due to the chemical reaction driving it to the electrodes. The
open-circuit voltage, i.e. the potential difference between A and B
when no current is drawn by connecting the wire, is called the
electromotive force, or
emf.
We denote it by e. When a
current flows through the battery, the
terminal
voltage = VA - VB is usually
less than e. This is because of the
internal resistance,
rb, of the battery. From the diagram, it is clear that the
resistance of the wire (and whatever devices connected to the wire),
R, and rb are in
The
open-circuit voltage, i.e. the potential difference between A and B
when no current is drawn by connecting the wire, is called the
electromotive force, or
emf.
We denote it by e. When a
current flows through the battery, the
terminal
voltage = VA - VB is usually
less than e. This is because of the
internal resistance,
rb, of the battery. From the diagram, it is clear that the
resistance of the wire (and whatever devices connected to the wire),
R, and rb are in