Kirchhoff Rules

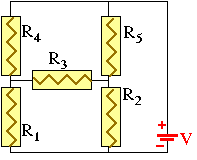There are circuits, such as the one on the right, that cannot be reduced to an equivalent series or parallel resistance. What to do? Fortunately, there are two rules, named after Kirchhoff, that enable us to solve all circuits containing any arbitrary arrangement of resistors and batteries (or, more generally, sources of external potential differences). Kirchhoff's rules, in the form they are stated here, do not apply to circuits containing "active components" (e.g. transistors that amplify), or "non Ohmic" components -- they work only with so called "linear", (or "passive") components.

Rule 1:

The net current flowing into any junction must equal to the net current flowing out of that junction.

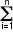I_i = 0

This tells us that the sum of all currents I_i, i = 1, ..., n, at any given junction is 0, where we count currents flowing into a point as positive, and currents flowing out of the point as negative. Basically, this tells us that "what goes in must come out" -- that's just the principle of conservation of charge.

Rule 2:

The sum over all potential differences around any closed loop must sum to zero. 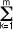V_k- 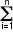I_iR_i= 0
where the individual V_k, k = 1, ..., m, are the potentials supplied by the batteries in a given loop; and I_i, i = 1, ..., n are the currents flowing through the resistors R_i, resulting in voltage drops across the resistors in that same loop.

If you multiply both of these quantities with the current flowing in the respective arms of the loop, you realize that the first is the power generated in the batteries or other sources of external potential difference, and the second is just the power dissipated. So this rule is basically a statement of the principle of conservation of energy.

How can one use Kirchhoff rules?

In a complicated circuit, like the one above, you list which quantities are unknown (usually the currents flowing through different wires, or potential between two points).
Now you need to use Kirchhoff rules to find as many equations as there are unknowns.
Once you have a system of N equation for your N unknowns, then you can solve it with standard linear algebra. (You may not know what the phrase "standard linear algebra" means, but we will discuss some examples in detail, and you will recognize the general procedure.)