Power Dissipation

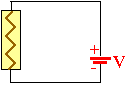The simplest possible direct current circuit is the one shown in the diagram. The battery is symbolized by the two parallel lines of different lengths. The resistance of the wire is shown as the box with the zigzag line. The thin black leads connecting the two are assumed to have no resistance.

An important thing to notice is that in any circuit, no matter how complicated, one end of the resistor is always at a higher potential than the other end. Otherwise a steady current would not flow. This difference is usually referred to as the potential drop across the resistance.

We can now derive an expression for the power dissipated in a resistor. Let's do it two ways, calculus and non-calculus:

• Non-calculus:
  When a current flows through a resistance, charges flow across the potential drop across the resistance. To send a charge q across the potential drop V, the work done by the battery is V$\cdot$ q. This would have increased the energy of the charges, except that they have to give up this energy to heat dissipation, in the process of ramming through the collisions, described earlier. The heat dissipated is then

  W = V $\cdot$ q = V $\cdot$ I $\cdot$ t = I2 R t =	V2 $\cdot$ t
  	R

  Where the last two steps were obtained from using Ohm's law. The Power dissipated is then

  P =	W	= V$\cdot$ I = I2R =	V2
  	t		R

• Calculus:
  Since the resistor is connected to the battery, the potential drop across the resistor must be V, and from Ohm's Law we get:
  V = I$\cdot$ R. We can calculate the work, dW, required to transport an infinitesimally small charge, dq, across the resistor. It is equal to the change in potential energy, dU, which we have learned to be related to the potential via: dW = dU = V dq

  Since I = dq/dt, and therefore dq = I dt, it follows: dW = V I dt. By definition, the power, P, is P = dW/dt, and thus we get our result:

  P =	dW	= V I = I2 R =	V2
  	dt		R

  where the last two steps were obtained by using Ohm's Law.

• As usual: both derivations give the same result.

You may think that power dissipation is always a problem in circuits. For computers this is true. One of the limits to the computing power of supercomputers is given from the fact that the power dissipated by the circuitry in the form of heat has to be removed from the computer. But in some appliances the heat from power dissipation is very much desirable and in fact their main purpose. The blow-dryer shown here is a good example. The red arrow points to the heating elements that are simply heated by the power dissipated in the relatively high resistance of the heating wire.

The Unit kilowatt-hour commonly used for electrical consumption: Watt is a unit of power, Watt-hour, therefore, must be a unit of power times time, that is energy. This is the unit in which our domestic electricity consumption is measured.

For this and other power units, you may want to use our JavaScript unit conversion engine.

© MultiMedia Physics 2000