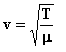
Calculation of Natural Frequencies

If we know the wave velocity, then we can calculate the natural frequencies of waves on strings. If a string is under a tension T (string tension is a force, remember?) and has a mass density m,

\[ \rm \mathbf{ \mu = \frac{M}{L}} \]

where L = length of the string and M = the mass of the string, then the wave velocity is

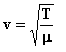
The natural frequencies are given by

\[ \rm \mathbf{f_{n} = \frac{nv}{2L}} \]

and inserting this result for the velocity yields:

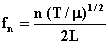
This means that the natural frequencies on a string are proportional to the square-root of the tension the string is under. You can verify this with a very simple experiment: Tie a string to a doorknob, and pull on it so that it is under tension. Then pluck it. You will hear a tone. Pulling harder on the string will raise the tone.