If you have measured values for the quantities X, Y, and Z, with uncertainties dX, dY, and dZ, and your final result, R, is the sum or difference of these quantities, then the uncertainty dR is:
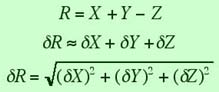
Here the upper equation is an approximation that can also serve as an upper bound for the error. Please note that the rule is the same for addition and subtraction of quantities.
|
Example: and the error in the displacement is: |
In the same way as for sums and differences, we can also state the result for the case of multiplication and division:
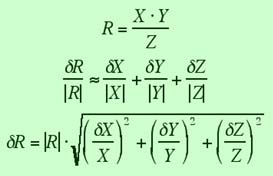
Again the upper line is an approximation and the lower line is
the exact result for independent random uncertainties in the
individual variables. And again please note that for the purpose
of error calculation there is no difference between multiplication
and division.
|
Example: and the uncertainty in the velocity is: |
What if you have measured the uncertainty in an observable X, and you need to multiply it with a constant that is known exactly? What is the error then? This is easy: just multiply the error in X with the absolute value of the constant, and this will give you the error in R:
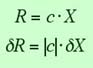
If you compare this to the above rule for multiplication of two
quantities, you see that this is just the special case of that
rule for the uncertainty in c, dc =
0.
|
Example: The uncertainty in the fall time is then: |
What if there is a dependence of the result on the maesured quantity X that is not described by simple multiplications or additions? We will state the general answer for R as a general function of one or more variables below, but will first cover the specail case that R is a polynomial function of one variable X.
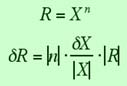
You see that this rule is quite simple and holds for positive
or negative numbers n, which can even be non-integers.
And finally, we can express the uncertainty in R for general functions of one or mor eobservables. If R is a function of X and Y, written as R(X,Y), then the uncertainty in R is obtained by taking the partial derivatives of R with repsect to each variable, multiplication with the uncertainty in that variable, and addition of these individual terms in quadrature.
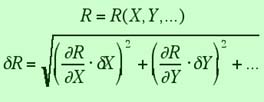
All rules that we have stated above are actually special cases of this last rule. We leave the proof of this statement as one of those famous "exercises for the reader".