Elastic Collisions in 2D or 3D
We now want to study the elastic collision of two bojects in two
or three spatial dimensions. For the one-dimensional case of an
elastic collision, we have worked our a general solution. This is
possible, because there are two unknowns (v3 and
v4) and two equations (momentum conservation and kinetic
energy conservation) to determine them. In general one needs at least
as many equations as there are unknowns to solve a system of
equations.
- In 2 dimensions, we have 4 unknowns (2 components of
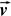 3
and
3
and 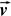 4
each), but only 3 equations for the conserved quantities
4
each), but only 3 equations for the conserved quantities
(Ekin, Px, and Py).
- In 3 dimensions, we have 6 unknowns (3 components of
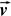 3
and
3
and 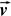 4
each), but only 4 equations for the conserved quantities
4
each), but only 4 equations for the conserved quantities
(Ekin, Px, Py,
Pz).
- There is therefore no general unique solution without imposing
additional constraints. (Makes billiards interesting!)
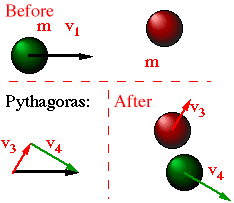 Interesting
case: m1= m2= m, and
Interesting
case: m1= m2= m, and 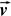 2=
0
2=
0
- Conserved kinetic energy:
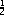 mv12=
mv12=
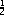 mv32
+
mv32
+ 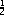 mv42
mv42
- Dividing out m/2 results in:
- v12= v32 +
v42
- This means (Pythagoras) that there will be a 90° angle
between
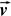 3
and
3
and 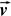 4.
4.

© MultiMedia Physics, 1999
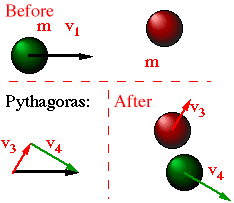 Interesting
case: m1= m2= m, and
Interesting
case: m1= m2= m, and 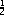 mv12=
mv12=
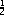 mv32
+
mv32
+ 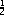 mv42
mv42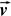 3
and
3
and 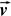 4.
4.