Photoelectric Effect
 If a
metal surface is illuminated by visible or ultraviolet radiation,
electrons are released - provided the frequency of the radiation
exceeds a critical threshold. The number of electrons increases with
the intensity of radiation, but the energy of the electrons does not.
This effect was explained by Einstein assuming that the
electromagnetic radiation is quantized.
If a
metal surface is illuminated by visible or ultraviolet radiation,
electrons are released - provided the frequency of the radiation
exceeds a critical threshold. The number of electrons increases with
the intensity of radiation, but the energy of the electrons does not.
This effect was explained by Einstein assuming that the
electromagnetic radiation is quantized.
In Einstein's model, it was assumed that a minimal energy, the
work function $\phi$, must be given to an
electron before it can escape from the surface of the metal. The work
function is a property of a given metal and is in the range 1 to 10
eV. No emission occurs unless hn >
f, but when the energy exceeds the work
function, the electron can be emitted with kinetic energy (KE) as
large as:
KEmax = h$\nu$ -
$\phi$.
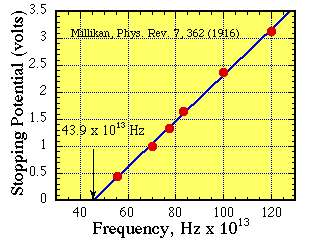
The value of KEmax can be measured using a simple
circuit in which light of frequency $\nu$ is
shone on a metal surface that has a retarding voltage Vr
applied to oppose the emission of electrons.
We steadily increase Vr until the current vanishes. At
that point the voltage will be the critical retarding voltage,
Vro, where
eVro = h$\nu$ -
$\phi$ = KEmax
where e is the charge of an electron, e =
1.6·10-19 C.
The current vanished when
Vr > Vro
©
MultiMedia Physics
2000
 If a
metal surface is illuminated by visible or ultraviolet radiation,
electrons are released - provided the frequency of the radiation
exceeds a critical threshold. The number of electrons increases with
the intensity of radiation, but the energy of the electrons does not.
This effect was explained by Einstein assuming that the
electromagnetic radiation is quantized.
If a
metal surface is illuminated by visible or ultraviolet radiation,
electrons are released - provided the frequency of the radiation
exceeds a critical threshold. The number of electrons increases with
the intensity of radiation, but the energy of the electrons does not.
This effect was explained by Einstein assuming that the
electromagnetic radiation is quantized.