Diffraction by a Single Slit

If we illuminate a slit with light of wavelength $\lambda$ comparable to the width of the slit b, a diffraction pattern will be produced. This pattern is comprised of a bright central band bounded by dark and bright bands of diminishing intensity as shown in the picture on the right. If d is much bigger than the wave length of the light, then the pattern on the screen is just the slit its self. As d is decreased, the screen shows a diffraction pattern. The central band widens and the minima and secondary maxima move out. The angles of the diffraction minima are given by

\[ \rm \mathbf{ \theta_{n} = \frac{n \lambda}{b}; n = 1, 2, 3, ...} \]

If we project the diffraction pattern on a screen a distance D away, the separation x_m between the n^th minimum and the center of the pattern is given by

\[ \rm \mathbf{x_{n} = \frac{n D \lambda}{b}; n = 1, 2, 3, ...} \]

and the distance to the first minimum from the center is

\[ \rm \mathbf{ \Delta x = \frac{D \lambda}{b}} \]

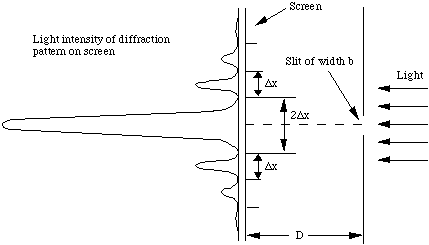
The width of the central maximum is given by 2Dx.