Capacitors in Parallel

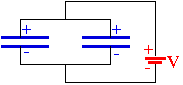When two or more capacitors are connected in parallel, all positively charged plates are connected together and are thus at the same potential. The same is true for the other plates: all negatively charged plates are connected together and are thus at the same potential. Thus the potential drop for each of the capacitors is the same:

Also, the total charge is equal to the sum of the charges on each capacitor:

Now we we try to calculate the equivalent capacitance of this arrangement of parallel capacitors, which we will denote by C_p.

Since Q = C_pV, we get

where C_p is the equivalent capacitance of the capacitors in parallel, i.e. the capacitance that one capacitor would have to have, if we wanted to replace the capacitors in parallel by it.

From the last equation, we can cancel out the factor V and get for the equivalent capacitance of two capacitors connected in parallel:

Again, just as was the case for capacitors in series, we can also generalize this result to the case of n parallel capacitors:

© MultiMedia Physics 2000