Capacitors in Series

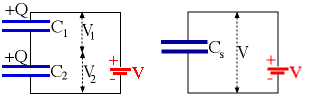
When two or more capacitors are connected in series, the "bottom" of one capacitor is connected to the "top" of the next one (see left diagram). If the positive plate of one has the charge Q, and the positive plate of the other also has the same charge Q.

This is a statement that is generally true: When two or more capacitors are connected in series, the charges are the same on each capacitor:

Also, the sum of the potential drop on each capacitor is equal to the total potential drop:

Let us call the equivalent capacitance of the series arrangement of these two capacitors C_s. Since the total charge Q and potential drop V are given, then the definition of the capacitance tells us that V = Q/C_s,V₁ = Q/C₁, V₂ = Q/C₂, and we get

where C_s is the equivalent capacitance of the capacitors in series.
From the last equation, we can cancel out the factor Q, and finally get for the equivalent capacitance of two capacitors connected in series:

Another way to write this formula for two capacitors is

Please note that the above arguments also easily extend to series of more than two capacitors. In the case that n capacitors are in series we have:

© MultiMedia Physics 2000