Equipotential Cases

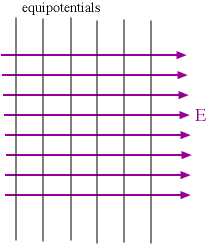
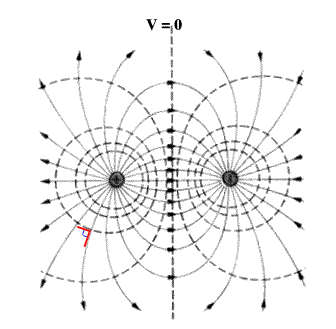
Here are two more cases for which we have shown the equipotential lines and the field lines.

On the left, we show the case for a constant electric field. The equipotentials (gray lines) for a uniform electric field (purple arrows) are equally spaced parallel lines, as can be seen in the upper figure. An electric field line can not have a component along an equipotential (if it did, a certain amount of work would be done on a test charge).

The dashed lines in the figure on the right are equipotentials. The solid lines are electric field lines for an electric dipole, as we have already seen from our applet.

Note that the two sets of lines are perpendicular everywhere. Again, this is a general result that always is true.

Any field has equipotential lines (or equipotential surfaces in 3d cases). Another such field is the field of gravity. Any sphere that encloses the Earth is a gravitational equipotential surface. You can now, for example, construct a sphere that is exactly 200 feet above sea level. Whereever the surface of the Earth intersects the surface of this imaginary sphere, marks an equipotential line of the gravitational field, i.e. all points at the same height above sea level lie on the same gravitational equipotential line

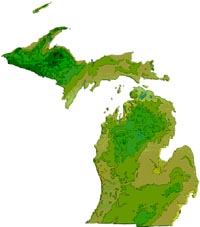
Here is an example of equipotential curves (the thin black lines between the areas of different colors); they are equipotentials for the gravitational field of the State of Michigan (Click on the picture to get a larger version). Actually each curve is 200 ft in height difference from the next, but everywhere on that curve the gravitational potential is a constant.