Potential of Charge Distributions

Since we already calculated a few electrostatic potential energies, we can calculate the electrostatic potential for these cases as well.

Potential due to a single charge:

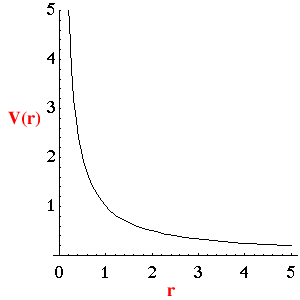
From the discussion of the last section, and the definition of V, for a charge Q at the origin, in a medium of permittivity $\epsilon$, the potential at a point is :

) = k · Q / r

This potential is also known as the Coulomb potential.

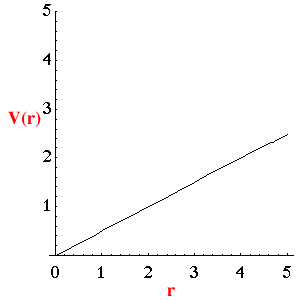
Potential in a constant electrostatic field:

Potential difference in a constant electric field: V_AB = - E $\Delta$r cosq

Therefore potential in a constant field is :

V(r) = - E r cos$\theta$

Potential at a point due to a number of charges:

The potential due to a single charge is a scalar. If we have a number of charges, the net potential at any point due to the entire charge distribution is found by simply adding the contribution of each charge, individually.

) = V₁(

) + V₂(

) + V₃(

) + ...

The potential at the point is due to one of the charges is unaffected by the presence of the other charges. That is why we can calculate the contribution at due to each charge separately, and simply make the algebraic sum. This is called the Principle of Superposition.