Standing Waves and Resonances

If you shake a rope or a hose, waves travel down to the fixed end and are reflected. These waves interfere with each other.

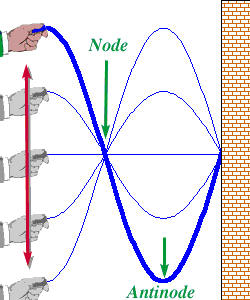
If you shake the rope at just the right frequency, the waves appear to stand still. These waves are called standing waves. Here is a little demonstration where a rope gets shaken just at the right frequency to excite standing waves:

The stationary points on the rope are called nodes. The waves cancel each other at these points. The points of maximum motion (largest positive and largest negative displacement) are called antinodes. Adjacent antinodes are separated by half a wavelength ($\lambda$/2) as are adjacent nodes.

One can generate standing waves on a rope or a string by driving the motion at the natural or resonant frequencies.

Most objects have natural frequencies of vibration. These natural frequencies are the ones that objects prefer to oscillate in. The term "resonant frequencies" refers to the fact that you can easily pump energy into these objects with external periodic driving forces at those frequencies.

It is a great challenge of engineering to construct structures that have no resonant frequencies in frequency ranges that can be excited by natural weather phenomena. On example of a structure where this was not done properly is the famous Tacoma Narrows bridge in the state of Washington. Periodic wind gusts excited the bridge at resonance and destroyed it.

While military formations enjoy marching in lockstep, prudent military commander always give orders for their troops to walk and not march across a bridge, for fear that the periodic stomping will excite a resonance in the bridge and collapse the structure.