Velocity and Acceleration in SHM

We have just given the general equation of motion of an object in simple harmonic motion,

x(t) = A sin(wt+d)

Since we have the displacement as a value of time, we can easily get the velocity and acceleration as a function of time, too. This can simply be done by taking the time derivative. If you have had calculus, you will indeed find the following easy to see. If not, please simply accept the result.

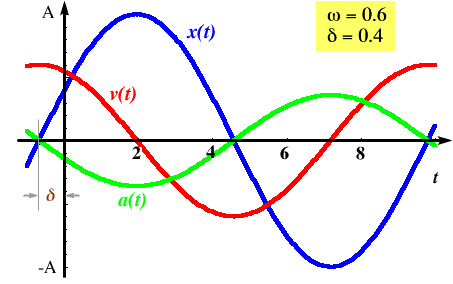
\[ \rm \mathbf{v(t) = \frac{dx}{dt} = A $\omega$ cos(\omega t + \delta)} \] \[ \rm \mathbf{a(t) = \frac{dv}{dt} = \frac{d^{2}x}{dt^{2}} = -A $\omega^{2}$ sin(\omega t + \delta)} \]

Note that A could be negative. Also note that x(t) and a(t) are out of phase by 180°, or p radians, while x(t) and v(t) are out of phase by 90°, or p/2 radians.

In this figure, we show the relationship between displacement, velocity, and acceleration for one choice of the angular frequency w (= 0.6) and the phase d (= 0.4). For a different choice of d, all three of these curves would be shifted to the left or right, but all by the same amount.

If we had started with our special initial conditions (x = maximum displacement at t = 0) we would have instead

x(t) = A cos(wt)
v(t) = -A w sin(wt)
a(t) = -A w²cos(wt)

where A is the initial displacement. Please not that all of the kinematic quantities, x, v, and a, all have the same phase shift d. This is the only influence that the phase has, even though the equations might at first look different to you. You can convince yourself of this fact by employing the trigonometric identities just mentioned.