Initial Conditions and Phase

We have earlier encountered the equation of motion for simple harmonic motion as a cosine function. This actually is only true for the special case that the object undergoing simple harmonic motion is at maximum elongation at time t=0. The general expression for SHM is

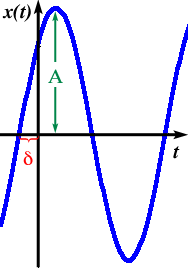
x(t) = A sin(wt+d)

where x(t) is the displacement, w is the frequency, and d is the phase. The units of phase have to be the same as that of wt (radians or degrees.) In the figure on the right, you can see what the constants A and d mean graphically.

Equations of motion containing sine and cosine expressions are the same except for the phase. In problems dealing with SHM, the phase is determined by the initial conditions.

A simplification that has been used throughout most of this chapter has been to choose the form

x(t) = A cos(wt)

for cases where the displacement is at a maximum at t=0. However, this is included as a special case of the general equation above, fixing the phase d to a value of p/2. One can understand this fact from the simple trigonometric identity

sin(wt+p/2) = cos(wt)

You could also select an initial condition where the equation of motion would be

x(t) = A sin(wt)

by chosing a phase of d = 0. This could be done by giving the oscillator initially 0 displacement but some nonzero value for the velocity.